A befektetési alapok szórása megmutatja, hogy mekkora kockázattal kell számolnunk az adott befektetési alap megvásárlásakor. Ez a pénzügyi világban leggyakrabban használt kockázati mutató. Sokak számára ismert, azonban nagyon kevesen tudják, hogyan kell valójában számolni, és pontosan mit is jelent.
Jelenleg a befektetési alapok szórásáról tájékozódhatunk például a BAMOSZ oldalán. Arról, hogy mennyire fontos a kockázatot és a múltbéli hozamokat együtt vizsgálni, már korábban írtam ebben a cikkben: A hozam és a kockázat.
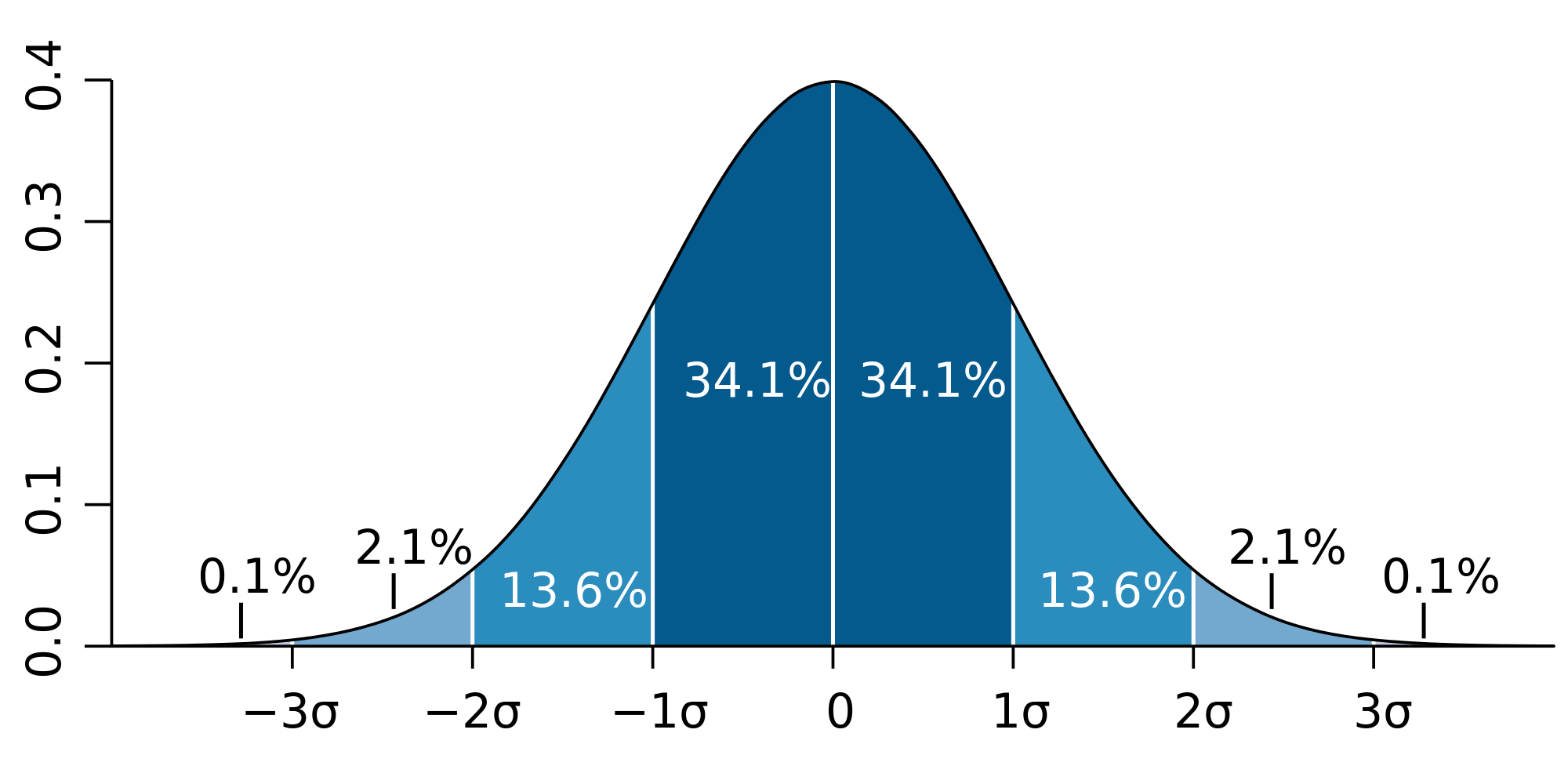
Az átlag sosem értelmezhető a szórás nélkül: a szórás megmutatja, hogy az egyes értékek átlagosan milyen mértékben térnek el az átlagtól. Ezt könnyű szemléltetni. Ha egy munkavállaló átlagosan nyolc órára ér be a munkahelyére, akkor az jelentheti azt, hogy:
1. Mindig pontosan érkezik.
2. Egyszer 6 órára, egyszer 10 órára ér be.
Az első esetben a szórás nulla, hiszen nincsen eltérés az átlagtól. Második esetben viszont a szórás 2 óra: átlagosan ennyivel jön korábban, vagy később, mint az átlag.
A szórás nagyon fontos befektetési alapok választásakor, valamint ebből számítják a Shapre mutatót is. A szórás befektetési alapoknál megmutatja, hogy milyen ingadozás várható az alap teljesítményében. A kérdés az, hogy az alap kockázata megfelel-e a te kockázatvállalási hajlandóságodnak. Minél hosszabb távra gondolkodsz, annál magasabb szórású alapokat is célszerű számításba venned. Rövid távra azonban kerülni kell a magas szórású alapokat.
Két befektetési alap közül az teljesített jobban a múltban,- kizárólag a hozamot és a szórást vizsgálva – amelyik ugyanakkora hozamot alacsonyabb szórás mellett ért el.
Befektetési alapok szórásának kiszámításához szükséges képlet
A szórás kiszámításához először is vesszük a teljes adatsort, és minden adatból kivonjuk a teljes adatsor átlagát. (Azaz minden napra vesszük az átlagtól való eltérést.) Az így kapott eltéréseket a négyzetre emeljük, majd mindet összeadjuk. Ezt a számot utána osztjuk az adatsor darabszáma mínusz eggyel. Ennek a számnak vesszük a négyzetgyökét.
Szórás képlet:
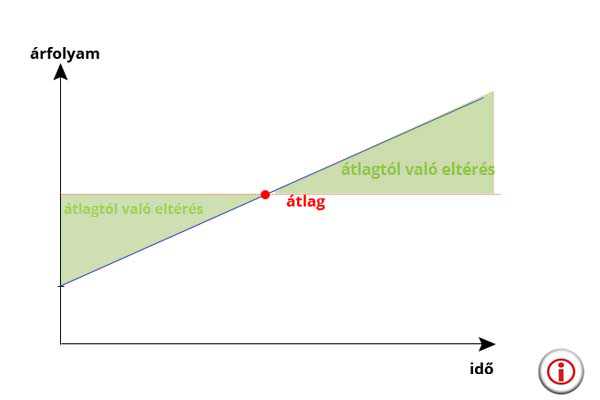
Nagyon fontos megjegyezni, hogy a közhiedelemmel ellentétben sok esetben a befektetési alapok szórása nem az árfolyamadatok szórását jelenti. Természetesen ezt a szórást is célszerű lehet kiszámolni, ha éppen arra vagyunk kíváncsiak, hogy miként ingadozott az árfolyam az elmúlt időben, azonban gyakrabban használt a napi hozamok szórásának kiszámítása. Ha az első esettel számolnánk, akkor egy egyenletesen emelkedő árfolyam szórása nem nulla, hanem egy időtávtól függő szám. Ezt könnyen beláthatjuk, ha megnézzük a következő grafikont:
Ezen a példán az alap árfolyama egyenletesen növekszik, azaz a hozamban nincsen szórás. Az árfolyam adatok azonban változnak, így az abból számolt átlag (pirossal jelölve) eltér a többi adattól, ami így az időtáv növekedésével egyre nagyobb szórást eredményez. Éppen ezért ez a számítás nem tükrözi a hozamunk ingadozását, mindössze az árfolyam változást jelzi. Ha így számolunk, akkor egy stabilan, (monoton) növekvő alap szórása is igen nagy lehet.
A befektetési alapok szórásának számítása a hozamokból
Tehát a fent leírtakkal szemben tegyük fel, hogy az adatsor nem a napi árfolyam, hanem a napi hozam. Ezt úgy kapjuk meg, hogy megnézzük mennyi volt az árfolyam az adott napon, és azt elosztjuk az előtte lévő napi árfolyammal (vesszük az arányát), majd kivonunk belőle egyet. Ha ezt szorozzuk százzal, akkor megkapjuk százalékban kifejezve a napi változást.
n-edik nap árfolyamváltozása: [fusion_builder_container hundred_percent=”yes” overflow=”visible”][fusion_builder_row][fusion_builder_column type=”1_1″ background_position=”left top” background_color=”” border_size=”” border_color=”” border_style=”solid” spacing=”yes” background_image=”” background_repeat=”no-repeat” padding=”” margin_top=”0px” margin_bottom=”0px” class=”” id=”” animation_type=”” animation_speed=”0.3″ animation_direction=”left” hide_on_mobile=”no” center_content=”no” min_height=”none”][Árfolyam (n) / Árfolyam (n-1)] – 1
Tehát minden napra ki kell számolni, hogy hány százalékot változott az előző naphoz képest, és ezeknek az adatoknak kell kiszámítani a szórását. Ezzel tehát nem az árfolyamváltozás szórását számoljuk ki valójában, hanem azt, hogy mekkora különbségek vannak átlagosan az egyes napi változások között. Ha tehát egy befektetési alap árfolyama stabilan 2%-ot növekszik, akkor a szórás nulla lesz. Ez logikus, hiszen egy 2%-ot fizető pénzpiaci befektetési alap szórása elméletileg nulla.
A befektetési alapok szórása tehát az átlagos napi változástól való átlagos eltérést mutatja meg.
A szórás adat évesítése
Ha mindez nem lenne elég, akkor még a számítás végén a kapott szórást évesíteni kellene, hogy össze tudjuk vetni az évesített hozam adatokkal. Azt tudjuk, hogy mennyi a napi szórás, de a kérdés az, hogy mondjuk egy év alatt mennyi lehet. Ezt úgy oldhatjuk meg, hogy megszorozzuk a kapott szórást gyök 252-vel, feltételezve, hogy 252 munkanap van egy évben. (Ha heti adatokkal dolgozunk, akkor gyök 52-vel szorozzunk!)
Így azonban már átlagos felhasználó nem túl sokat ért meg a szórásból, valójában azzal, hogy elolvastad ezt a bejegyzést már a befektetők 99%-nál többet tudsz a kockázati mutatókról. A legtöbben maximum azt látják, hogy az egyik több a másik kevesebb. Ha szeretnéd tudni az alapoknak a valódi szórását, és biztosra akarsz menni, akkor jobb, ha magadnak számolod ki: ahány honlap annyiféle számítás, és sokszor nem is közlik le, hogy pontosan mi alapján számolják, illetve milyen időtávra a szórást.
Ez elég félrevezető lehet, hiszen az elmúlt 1 év szórása egy befektetési alapnál nem fogja megmutatni neked, hogy mekkora szórásra kell számítanod, amikor mondjuk válság van, vagy éppen zuhan az alap értéke. Pedig pont ez a szórás mutató lényege.
Egy excelt, amiben kiszámolom többféle szórását egy Pioneer alapnak, itt tudsz letölteni: Befektetesi alap szoras szamitas minta
Két dolgot tehetsz: Kérj ingyenes tanácsadást az alábbi formon, vagy töltsd le az árfolyamadatokat, és számold ki magadnak a szórást úgy, ahogy az neked megfelel.
Szívesen tanulnál a pénzügyekről? Íme, egy 14 napos, ingyenes kihívás és tréning!
Szeretnél szakértői segítséget? Kérj valódi pénzügyi tanácsadást!
[/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]